Automatic sequence
An automatic sequence (or k-automatic sequence) is an infinite sequence of terms characterized by a finite automaton. The n-th term of the sequence is a mapping of the final state of the automaton when its input is the digits of n in some fixed base k.[1] A k-automatic set is a set of non-negative integers for which the sequence of values of its characteristic function is an automatic sequence: that is, membership of n in the set can be determined by a finite state automaton on the digits of n in base k.[2]
Contents |
Automaton point of view
Let q be an integer, and A = (E, φ, e) be a deterministic automaton where
also let A be a finite set, and π:E → A a projection towards A.
For each n, take m(n) = π(φ(e,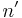 )) where
)) where 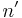 is n written in base q. Then the sequence m = m(1)m(2)m(3)... is called a q-automatic sequence.[1]
is n written in base q. Then the sequence m = m(1)m(2)m(3)... is called a q-automatic sequence.[1]
Substitution point of view
Let σ be a morphism of the free monoid E* with 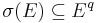 , and
, and 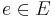 such that σ(e) begins by e. Let also be A and π as before. Then if
such that σ(e) begins by e. Let also be A and π as before. Then if 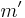 is a fixpoint of σ, that is to say
is a fixpoint of σ, that is to say 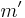 = σ(
= σ(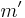 ), then m = π(
), then m = π(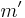 ) is a q-automatic sequence over A.[3]
) is a q-automatic sequence over A.[3]
1-automatic sequences
k-automatic sequences are normally only defined for k ≥ 2.[1] The concept can be extended to k = 1 by defining a 1-automatic sequence to be a sequence whose n-th term depends on the unary notation for n, that is (1)n. Since a finite state automaton must eventually return to a previously visited state, all 1-automatic sequences are eventually periodic.
Properties
For given k and r, a set is k-automatic if and only if it is kr-automatic. Otherwise, if h and k are multiplicatively independent, then a set is both h-automatic and k-automatic if and only if it is 1-automatic, that is, ultimately periodic.[4]
Examples
The following sequences are automatic:
- Thue-Morse sequence: take E = A = {0, 1}, e = 0, π = id, and σ such that σ(0) = 01, σ(1) = 10; we get the fixpoint 01101001100101101001011001101001... , which is in fact the Thue-Morse word. The n-th term is the parity of the base 2 representation of n and the sequence is thus 2-automatic.[1]
- Rudin–Shapiro sequence
- Baum–Sweet sequence
- Regular paperfolding sequence
Automatic real number
An automatic real number is a real number for which the base-b expansion is an automatic sequence.[5] All such numbers are either rational or transcendental.[6]
References
- ^ a b c d Allouche & Shallit (2003) p.152
- ^ Allouche & Shallit (2003) p.168
- ^ Allouche & Shallit (2003) p.175
- ^ Allouche & Shallit (2003) pp.345-350
- ^ Hejhal (1999) p.556
- ^ B. Adamczewski and Y. Bugeaud, "On the complexity of algebraic numbers. I. Expansions in integer bases", Ann. of Math. 165:2 (2007), pp. 547–565.
- Jean-Paul Allouche and Jeffrey Shallit Automatic Sequences Cambridge University Press 2003, ISBN 0-521-82332-3
- Dennis A. Hejhal, Emerging applications of number theory, The IMA volumes in mathematics and its applications 109, Springer, 1999, ISBN 0387988246
- J. H. Loxton, "Automata and transcendence", Chapter 13 of New Advances in Transcendence Theory, ed. A. Baker, Cambridge University Press 1988, ISBN 0521335450